 1) Se eu adicionar 8 à quantidade de carrinhos que possuo, ficarei com a mesma quantidade de carrinhos de meu irmão, se dos 28 que ele possui, for retirada a quantidade que eu possuo. Quantos carrinhos eu tenho?
1) Se eu adicionar 8 à quantidade de carrinhos que possuo, ficarei com a mesma quantidade de carrinhos de meu irmão, se dos 28 que ele possui, for retirada a quantidade que eu possuo. Quantos carrinhos eu tenho?
Primeiramente vamos assumir que x seja a quantidade de carrinhos que eu possuo. Vamos montar então a expressão matemática por partes.
Sendo x a quantidade de carrinhos que eu possuo, ao adicionar 8, ficarei com x + 8.
Do enunciado sabemos que ele tem 28 carrinhos e se subtrairmos deste número a quantidade que eu possuo (x), ficaremos com quantidade iguais. Então:
x + 8 = 28 - x
A partir daí devemos deixar a incógnita x isolada no lado direito, passando os coeficientes para o outro lado.
O x que está sendo subtraído no segundo membro, passará ao primeiro membro sendo adicionado.
x + x + 8 = 28
x mais x é igual a 2x, assim como uma laranja mais uma laranja é igual a duas laranjas.
2x + 8 = 28
Passemos agora o 8 que está sendo adicionado, para o outro lado, na operação inversa, ou seja, sendo subtraído:
2x = 28 - 8
Realizando a subtração:
2x = 20
O coeficiente 2 que está multiplicando a incógnita x, passará para o outro membro dividindo o termo 20:
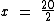
Realizando a divisão encontramos a raiz 10:
x = 10
Portanto:
 Eu tenho 10 carrinhos.
Eu tenho 10 carrinhos.
Sendo x a quantidade de carrinhos que eu possuo, ao adicionar 8, ficarei com x + 8.
Do enunciado sabemos que ele tem 28 carrinhos e se subtrairmos deste número a quantidade que eu possuo (x), ficaremos com quantidade iguais. Então:
x + 8 = 28 - x
A partir daí devemos deixar a incógnita x isolada no lado direito, passando os coeficientes para o outro lado.
O x que está sendo subtraído no segundo membro, passará ao primeiro membro sendo adicionado.
x + x + 8 = 28
x mais x é igual a 2x, assim como uma laranja mais uma laranja é igual a duas laranjas.
2x + 8 = 28
Passemos agora o 8 que está sendo adicionado, para o outro lado, na operação inversa, ou seja, sendo subtraído:
2x = 28 - 8
Realizando a subtração:
2x = 20
O coeficiente 2 que está multiplicando a incógnita x, passará para o outro membro dividindo o termo 20:
Realizando a divisão encontramos a raiz 10:
x = 10
Portanto:
 Eu tenho 10 carrinhos.
Eu tenho 10 carrinhos. 2) Comprei 7,5kg de um produto e recebi um troco de R$ 1,25. Caso eu tivesse comprado 6kg, o troco teria sido de R$ 5,00. Quanto dei em dinheiro para pagar a mercadoria?
2) Comprei 7,5kg de um produto e recebi um troco de R$ 1,25. Caso eu tivesse comprado 6kg, o troco teria sido de R$ 5,00. Quanto dei em dinheiro para pagar a mercadoria?
Digamos que p seja o preço por kg da mercadoria.
Como em ambos os casos eu teria um troco a receber, então o valor que eu
dei em pagamento seria igual à massa comprada vezes o preço por kg mais o troco nas duas situações. Teríamos então:
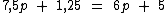
O 6p que está sendo somado no segundo membro, passará ao primeiro membro sendo subtraído, ao mesmo tempo em que o 1,25 à esquerda que está sendo somado passará à direita subtraindo:
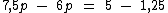
Realizando as subtrações:
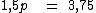
O coeficiente 1,5 que está multiplicando a incógnita p irá para o outro lado dividindo o termo 3,75:
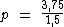
Que dividindo dá:
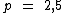
Tomemos então o primeiro membro da equação inicial
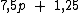
Ele representa quanto me custou o produto mais quanto recebi de troco, ou seja, quanto dei em dinheiro para o pagamento. Vamos então substituir p pelo valor encontrado de 2,5 e realizar os cálculos:
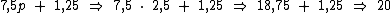
Portanto:
 Eu dei R$ 20,00 em dinheiro para o pagamento da mercadoria.
Eu dei R$ 20,00 em dinheiro para o pagamento da mercadoria.
O 6p que está sendo somado no segundo membro, passará ao primeiro membro sendo subtraído, ao mesmo tempo em que o 1,25 à esquerda que está sendo somado passará à direita subtraindo:
Realizando as subtrações:
O coeficiente 1,5 que está multiplicando a incógnita p irá para o outro lado dividindo o termo 3,75:
Que dividindo dá:
Tomemos então o primeiro membro da equação inicial
Ele representa quanto me custou o produto mais quanto recebi de troco, ou seja, quanto dei em dinheiro para o pagamento. Vamos então substituir p pelo valor encontrado de 2,5 e realizar os cálculos:
Portanto:
 Eu dei R$ 20,00 em dinheiro para o pagamento da mercadoria.
Eu dei R$ 20,00 em dinheiro para o pagamento da mercadoria. 3) A soma da minha idade, com a idade de meu irmão que é 7 anos mais velho que eu dá 37 anos. Quantos anos eu tenho de idade?
3) A soma da minha idade, com a idade de meu irmão que é 7 anos mais velho que eu dá 37 anos. Quantos anos eu tenho de idade?
Partamos do princípio que a minha idade seja igual a x. Como o meu irmão tem 7 anos a mais que eu, então ele tem x + 7 anos de idade. Como a soma das idades é de 37 anos, podemos escrever a seguinte sentença:
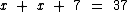
Ou seja:
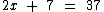
Passando para o outro lado o 7 como subtraindo, já que ele se encontra adicionando no primeiro membro, temos:
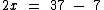
Realizando a subtração:
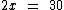
Passando o multiplicador 2 para a direita como divisor:
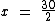
Que dividindo dá:
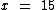
Portanto:
 Eu tenho 15 anos de idade.
Eu tenho 15 anos de idade.
Ou seja:
Passando para o outro lado o 7 como subtraindo, já que ele se encontra adicionando no primeiro membro, temos:
Realizando a subtração:
Passando o multiplicador 2 para a direita como divisor:
Que dividindo dá:
Portanto:
 Eu tenho 15 anos de idade.
Eu tenho 15 anos de idade. 4) Tenho a seguinte escolha: Ou compro 20 unidades de um produto com todo o dinheiro que tenho, ou compro apenas 14 unidades e ainda me sobra um troco de R$ 30,00. Qual o valor unitário deste produto?
4) Tenho a seguinte escolha: Ou compro 20 unidades de um produto com todo o dinheiro que tenho, ou compro apenas 14 unidades e ainda me sobra um troco de R$ 30,00. Qual o valor unitário deste produto?
Vou chamar de x o preço da unidade deste produto.
A partir do enunciando chegamos à seguinte equação:
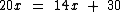
O termo 20x se refere às 20 unidades do produto multiplicado pelo seu valor unitário.
Sabemos que isto é igual a 14 unidades do produto multiplicado pelo seu valor unitário, mais 30 reais de troco, ou seja, 14x + 30.
Vamos passar o 14x para o primeiro membro, lembrando que por estar sendo adicionado, ele passará subtraindo:
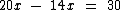
Ao fazermos a subtração:
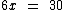
Passamos o 6 para o outro lado, dividindo já que ele está multiplicando:
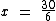
Que dividindo dá:
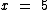
Portanto:
 O valor unitário deste produto é de R$ 5,00.
O valor unitário deste produto é de R$ 5,00.
A partir do enunciando chegamos à seguinte equação:
O termo 20x se refere às 20 unidades do produto multiplicado pelo seu valor unitário.
Sabemos que isto é igual a 14 unidades do produto multiplicado pelo seu valor unitário, mais 30 reais de troco, ou seja, 14x + 30.
Vamos passar o 14x para o primeiro membro, lembrando que por estar sendo adicionado, ele passará subtraindo:
Ao fazermos a subtração:
Passamos o 6 para o outro lado, dividindo já que ele está multiplicando:
Que dividindo dá:
Portanto:
 O valor unitário deste produto é de R$ 5,00.
O valor unitário deste produto é de R$ 5,00. 5) O volume de chuvas na minha região foi de 30 ml nos dois últimos dias. Sabe-se que ontem choveu o dobro da quantidade que choveu hoje. Qual foi o volume de chuva de hoje?
5) O volume de chuvas na minha região foi de 30 ml nos dois últimos dias. Sabe-se que ontem choveu o dobro da quantidade que choveu hoje. Qual foi o volume de chuva de hoje?
Chamemos de v o volume da chuva hoje.
Do enunciando tiramos que 2v corresponde ao volume de chuva de ontem, assim como 30 é o volume total. Podemos então montar à seguinte equação:
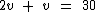
Somando os termos do primeiro membro temos:
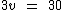
Passando o 3 para o outro lado, como divisor já que ele é um multiplicador:
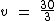
Ao dividirmos:
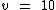
Portanto:
 O volume de chuva de hoje foi de 10 ml.
O volume de chuva de hoje foi de 10 ml.
Do enunciando tiramos que 2v corresponde ao volume de chuva de ontem, assim como 30 é o volume total. Podemos então montar à seguinte equação:
Somando os termos do primeiro membro temos:
Passando o 3 para o outro lado, como divisor já que ele é um multiplicador:
Ao dividirmos:
Portanto:
 O volume de chuva de hoje foi de 10 ml.
O volume de chuva de hoje foi de 10 ml. 6) Qual é o conjunto solução da equação 4x - 8 = 10?
6) Qual é o conjunto solução da equação 4x - 8 = 10?
Portanto:
 S = { 4,5 }.
S = { 4,5 }. 7) Qual é a raiz da equação 7x - 2 = -4x + 5?
7) Qual é a raiz da equação 7x - 2 = -4x + 5?
Portanto:
 7/11 é a raiz da equação.
7/11 é a raiz da equação. 8) U = { -5, 0, 3 } é o conjunto universo da equação 6x + 18 = 0. Qual é o conjunto solução desta equação?
8) U = { -5, 0, 3 } é o conjunto universo da equação 6x + 18 = 0. Qual é o conjunto solução desta equação?
Portanto:
 S = {} é o conjunto solução (conjunto vazio), pois -3 não pertence ao conjunto universo.
S = {} é o conjunto solução (conjunto vazio), pois -3 não pertence ao conjunto universo. 9) Encontre o conjunto verdade da equação -2x = -4 + 3x?
9) Encontre o conjunto verdade da equação -2x = -4 + 3x?
Portanto:
 V = {4/5} é o conjunto solução da equação.
V = {4/5} é o conjunto solução da equação. 10) 7 é raiz da equação x + 5 = 2?
10) 7 é raiz da equação x + 5 = 2?
Portanto:
 Não, pois -3 é que é a raiz desta equação.
Não, pois -3 é que é a raiz desta equação.